Posição em mais dimensões¶
- Posição no espaço ao longo de uma reta (1D): $x$.
- Posição no espaço 2D ou 3D: $\vec{r}$
- $\vec{r}$: Vetor posição, ou deslocamento em rel. à origem$$\vec{r} = x\hat{i}+y\hat{j}+z\hat{k}$$$x$, $y$ e $z$ são as coordenadas associadas à $\vec{r}$
ax = plt.axes()
pcoord = (0.5, 0.6)
# Vetores posição
p = vector2D(origin=o, dxdy=pcoord, label=r'$\vec{r}$')
p.plot(ax); p.plot_label(ax, distance=0.15)
plot(*p.tip, 'ro'); text(*(p.tip+(0.05, 0)), 'P')
xaxis = vector2D(origin=o,dxdy=(0.9,0), label=r'$x$')
xaxis.plot(ax); xaxis.plot_label(ax, relative_position=0.9, distance=0.05)
yaxis = vector2D(origin=o,dxdy=(0,0.9), label=r'$y$')
yaxis.plot(ax); yaxis.plot_label(ax, relative_position=0.9, distance=-0.05)
xlim(0,1); ylim(0,1)
axis('off'); ax.set_aspect('equal')
Movimento em mais dimensões¶
- Consideramos a posição variando no tempo:$$\vec{r}(t) = x(t)\hat{i}+y(t)\hat{j}+z(t)\hat{k}$$
ax = plt.axes()
pcoord = (0.5, 0.6)
p = vector2D(origin=o, dxdy=pcoord, label=r'$\vec{r}(t)$')
p.plot(ax); p.plot_label(ax, distance=0.15)
plot(*p.tip, 'ro'); text(*(p.tip+(0.05, 0)), 'P')
xaxis = vector2D(origin=o,dxdy=(0.9,0), label=r'$x$')
xaxis.plot(ax); xaxis.plot_label(ax, relative_position=0.9, distance=0.05)
yaxis = vector2D(origin=o,dxdy=(0,0.9), label=r'$y$')
yaxis.plot(ax); yaxis.plot_label(ax, relative_position=0.9, distance=-0.05)
t=linspace(0,2,250)
x_curve=p.tip[0] + (t-1)*cos(t-3)
y_curve=p.tip[1] + (t-1)*sin(4*t)
plot(x_curve, y_curve, '--')
xlim(0,1); ylim(0,1)
axis('off'); ax.set_aspect('equal')
Grandezas do movimento¶
- Vetor deslocamento: $\Delta\vec{r}=\vec{r}_2-\vec{r}_1$
- Vetor velocidade média: $\bar{\vec{v}}=\frac{\Delta\vec{r}}{\Delta t}=\frac{\vec{r}_2-\vec{r}_1}{t_2-t_1}$
- Vetor velocidade instantânea: $\vec{v}=\lim_{\Delta t \rightarrow 0}\frac{\Delta\vec{r}}{\Delta t}$
- A velocidade instantânea é tangente a trajetória!
f, (ax1, ax2) = plt.subplots(1, 2)
ax = ax1
#r1
pcoord = (0.5, 0.6)
p = vector2D(origin=o, dxdy=pcoord, label=r'$\vec{r}_1$')
p.plot(ax); p.plot_label(ax, distance=0.07)
ax.plot(*p.tip, 'ro');
#r2
tp2 = 1.2
p2coord = (p.tip[0]+(tp2-1), p.tip[1]-(tp2-1)*tp2**2)
p2 = vector2D(origin=o, dxdy=p2coord, label=r'$\vec{r}_2$')
ratio = sqrt((p2.dxdy[0]**2+p2.dxdy[1]**2)/(p2.tip[0]**2+p2.tip[1]**2)) # Correção do tamanho do vetor
p2.polar = (p2.polar[0]*ratio, p2.polar[1])
p2.plot(ax); p2.plot_label(ax, distance=-0.07)
ax.plot(*p2.tip, 'ro');
#curva
t=linspace(0,2,250)
x_curve=p.tip[0] + (t-1)
y_curve=p.tip[1] - (t-1)*t**2
ax.plot(x_curve, y_curve, '--')
#deslocamento
disp = vector2D(origin=p.tip, dxdy=p2.tip-p.tip, label=r'$\Delta\vec{r}$')
disp.plot(ax); disp.plot_label(ax, distance=0.07)
xaxis = vector2D(origin=o,dxdy=(0.9,0), label=r'$x$')
xaxis.plot(ax); xaxis.plot_label(ax, relative_position=0.9, distance=0.05)
yaxis = vector2D(origin=o,dxdy=(0,0.9), label=r'$y$')
yaxis.plot(ax); yaxis.plot_label(ax, relative_position=0.9, distance=-0.05)
ax.set_xlim(0,1); ax.set_ylim(0,1)
ax.axis('off'); ax.set_aspect('equal')
ax = ax2
#r
pcoord = (0.5, 0.6)
p = vector2D(origin=o, dxdy=pcoord, label=r'$\vec{r}_1$')
p.plot(ax); p.plot_label(ax, distance=0.07)
ax.plot(*p.tip, 'ro');
#curva
t=linspace(0,2,250)
x_curve=p.tip[0] + (t-1)
y_curve=p.tip[1] - (t-1)*t**2
t_deriv = 1
drdt = (1, -3*t_deriv**2+2*t_deriv)
v = vector2D(origin=p.tip, dxdy=drdt, label=r'$\vec{v}$')
v.polar=(0.3, v.polar[1])
v.plot(ax); v.plot_label(ax, distance=0.05)
ax.plot(x_curve, y_curve, '--')
xaxis = vector2D(origin=o,dxdy=(0.9,0), label=r'$x$')
xaxis.plot(ax); xaxis.plot_label(ax, relative_position=0.9, distance=0.05)
yaxis = vector2D(origin=o,dxdy=(0,0.9), label=r'$y$')
yaxis.plot(ax); yaxis.plot_label(ax, relative_position=0.9, distance=-0.05)
ax.set_xlim(0,1); ax.set_ylim(0,1)
ax.axis('off'); ax.set_aspect('equal')
Cálculo de $\vec{v}$¶
Em termos de vetores unitários,
Aceleração $\vec{a}$¶
- Definição similar à de $\vec{v}$.
- Aceleração média: $\bar{\vec{a}}=\frac{\Delta\vec{v}}{\Delta t}$,
- Aceleração instantânea: $\vec{a}=\frac{d\vec{v}}{dt}$.
Intuição sobre a aceleração¶
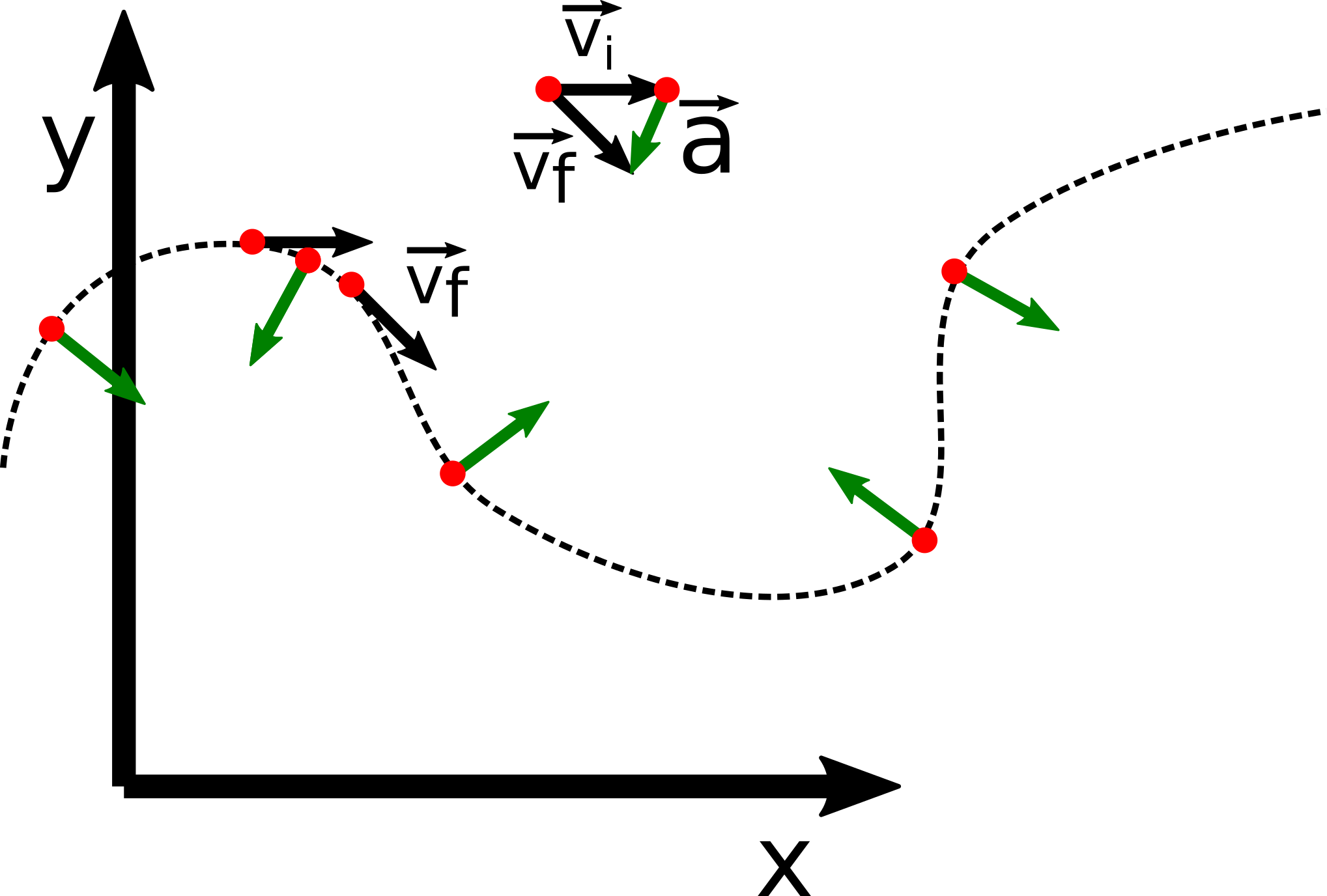
Exemplo: movimento com $\vec{v}=$ constante¶
Sejam $\begin{cases} x(t)=1+2t,\\ y(t)=2+3t, \end{cases}$, com $x$ e $y$ em m, e $t$ em s. Representar $x(t)$, $y(t)$ e o movimento no plano $x y$
Este caso admite representar $y$ como função de $x$: $$y=y(x)=2 + 3 \left(\frac{x-1}{2}\right)=\frac{1}{2}+\frac{3}{2}x$$
Representação gráfica do problema anterior¶
$\begin{cases} x(t)=1+2t,\\ y(t)=2+3t, \end{cases}$, com $x$ e $y$ em m, e $t$ em s.
t = linspace(-3,3,100)
x = 1+2*t
y = 2+3*t
plot(x,y)
xlabel('x')
ylabel('y')
grid()
Exemplo: movimento com $\vec{a}=\vec{\text{cte}}$¶
Sejam $\begin{cases} x(t)=-1+10t-2t^2,\\ y(t)=2-3t+t^2, \end{cases}$, com $x$ e $y$ em m, e $t$ em s.
Representar $x(t)$, $y(t)$ e o movimento no plano $x y$
Este caso não admite representar $y$ como função de $x$! A parametrização (representação em termos de $t$) é importante!
Representação gráfica¶
Sejam $\begin{cases} x(t)=-1+10t-2t^2,\\ y(t)=2-3t+t^2, \end{cases}$, com $x$ e $y$ em m, e $t$ em s.
t = linspace(-0.5,4,100)
x = -1+10*t-2*t**2
y = 2-3*t+t**2
plot(x,y)
xlabel('x')
ylabel('y')
grid()
Movimento sob aceleração constante ($\vec{a}=\vec{\text{cte}}$ )¶
Se $\vec{a}=\vec{\text{cte}}$, então $\begin{cases}a_x=\text{cte}\\a_y=\text{cte}\\a_z=\text{cte}\end{cases}$. Velocidades $\rightarrow$ $\begin{cases}v_x=v_{0x}+a_x t,\\v_y=v_{0y}+a_y t,\\v_z=v_{0z}+a_z t.\end{cases}$
Coordenadas $\rightarrow$ $\begin{cases}x=x_0+v_{0x}t+a_x \frac{t^2}{2},\\y=y_0+v_{0y}t+a_y \frac{t^2}{2},\\z=z_0+v_{0z}t+a_z \frac{t^2}{2}.\end{cases}$
Representação em termos de vetores:¶
\begin{align} \vec{v} &= v_x\hat{i}+v_y\hat{j}+v_z\hat{k},\\ &= v_{0x}\hat{i}+v_{0y}\hat{j}+v_{0z}\hat{k} + a_x t\hat{i}+a_y t\hat{j}+a_z t\hat{k},\\ &= \vec{v}_0+\vec{a} t.\\ \end{align}Exemplo: é possível eliminar o tempo?¶
- Atenção! Não é possível fazer como em 1D, onde $t=\frac{v-v_0}{a}$. Não existe "divisão" entre vetores.
- Eq. de Torricelli envolve quadrados das velocidades... Produto $\vec{v}\cdot\vec{v}$?
Movimento balístico¶
- Objeto lançado com $\vec{v}_0$ conhecido. Dados iniciais: $\begin{cases}v_0=\text{vel. do projétil,}\\\theta_0=\text{ângulo do lançamento.}\end{cases}$
- Sujeito à aceleração constante. Ex.: gravidade, $\vec{a}=-g\hat{j}$
- Como representar este movimento? Dados $v_0$ e $\theta_0$, qual o movimento do projétil?
- Assumimos que o movimento é independente em direções ortogonais. Nem sempre verdade. Ex.: Resistência do ar *acopla* $v_x$ e $v_y$.
Movimento horizontal¶
- Dados iniciais: $v_0$, $\theta_0$ e $\vec{a}=-g\hat{j}$.
- Movimento uniforme.
- $v_x=v_0\cos\theta_0$, $x(t)=x_0+v_0\cos\theta_0 t$.
Movimento vertical¶
- Dados iniciais: $v_0$, $\theta_0$ e $\vec{a}=-g\hat{j}$.
- Movimento uniformemente acelerado.
- $v_y(t)=v_{0y}+a_y t$, $y(t)=y_0+v_{0y} t + a_y \frac{t^2}{2}$.
- $a_y=-g$, $v_{0y}=v_0\sin\theta_0$
- $v_y(t)=v_0\sin\theta_0-g t$, $y(t)=y_0+v_0\sin\theta_0 t -g \frac{t^2}{2}$.
- Altura máxima quando $v_y=0$, ou $t^*=\frac{v_0}{g}\sin\theta_0$.
Equação da trajetória¶
- É possível escrever $y=y(x)$? I.e., "eliminar" o tempo?
- Note que $x-x_0=v_0\cos\theta_0 t$, ou $$t=\frac{x-x_0}{v_0\cos\theta_0},$$$y(t)=y_0+v_0\sin\theta_0 t -g \frac{t^2}{2}$ $ = y_0+v_0\sin\theta_0 \left(\frac{x-x_0}{v_0\cos\theta_0}\right) - \frac{g}{2}\left(\frac{x-x_0}{v_0\cos\theta_0}\right)^2$$=y_0+\tan\theta_0 \left(x-x_0\right) - \frac{g}{2v_0^2\cos^2\theta_0}\left(x-x_0\right)^2.$Trajetória parabólica! (Galileu) Quem é $\vec{v}(t)$? e $\theta(t)=\arctan{\frac{v_y}{v_x}}$?
Alcance¶
- Definido como o deslocamento em $x$ tal que $y$ retorna ao valor inicial $y_0$ $(y-y_0=0)$
- Seja o deslocamento na dir. x, $x-x_0=R$ (*range*), \begin{align} 0 &= \tan\theta_0 R - \frac{g}{2v_0^2\cos^2\theta_0}R^2\\ &= R \left(\tan\theta_0 - \frac{g}{2v_0^2\cos^2\theta_0}R\right) \end{align}
- Soluções: $R=0$ (trivial), ou $\tan\theta_0 - \frac{g}{2v_0^2\cos^2\theta_0}R=0$, $$ R = \frac{v_0^2}{g} 2\sin\theta_0\cos\theta_0 = \frac{v_0^2}{g} \sin2\theta_0$$.
- Atenção! Se a altura final do projétil não for igual a inicial, a distância percorrida ao longo da horizontal será diferente de $R$!
- Quando o alcance é máximo? R.: $\sin2\theta_0=1$, ou $2\theta_0=90^o$, $$\theta_0=45^o.$$
Altura máxima¶
- Simplificações: $x_0 = y_0 = 0$.
- $y=\tan\theta_0 x - \frac{g}{2v_0^2\cos^2\theta_0}x^2$. Para que valor $x=x^*$, $y(x)$ é máximo?
- $\frac{dy}{dx}=0$, ou $\tan\theta_0 - \frac{g}{v_0^2\cos^2\theta_0}x^*=0$, $$x^*=\frac{v_0^2}{g}\sin\theta_0\cos\theta_0.$$
- $y(x^*)=y_{max}\tan\theta_0\left(\frac{v_0^2}{g}\sin\theta_0\cos\theta_0\right) - \frac{g}{2v_0^2\cos^2\theta_0}\left(\frac{v_0^2}{g}\sin\theta_0\cos\theta_0\right)^2$, e $$y_{max}=\frac{v_0^2}{2g}\sin^2\theta_0.$$
- Outra forma de calcular: encontrar $t^*$ tal que $v_y(t^*)=0$.
Movimento circular uniforme (MCU)¶
- Importante para vários tipos de sistemas. Ex.: Carrossel, motores, engrenagens, rodas, satélites...
- Movimento de projéteis: $\begin{cases}\vec{a}=\vec{\text{cte}}\text{ em módulo e direção,}\\\vec{v}\text{ varia em módulo e direção.}\end{cases}$
- MCU: $\begin{cases}|\vec{a}|\text{ e } |\vec{v}|\text{ são ctes,}\\\text{direção de }\vec{v}\text{ e }\vec{a}\text{ variam.}\end{cases}$
Descrição do movimento¶
- $|\vec{v}_1|=|\vec{v}_2|=v=$cte.
- Espaço percorrido: $L=R\Delta \theta=v\Delta t$. ($\Delta \theta$ em radianos!)
ax = plt.axes()
# Círculo
theta = linspace(0,2*pi,100)
radius = 1
x = radius*cos(theta)
y = radius*sin(theta)
plot(x,y, 'k')
# Arco de círculo
dtheta = 0.4
DeltaTheta = linspace(-dtheta, dtheta, 20)
x = radius*cos(DeltaTheta)
y = radius*sin(DeltaTheta)
plot(x,y, 'm')
text(0.85,0, "L")
# Pontos indicando o início e o fim da trajetória
xi, yi = (x[0], y[0] )
xf, yf = (x[-1], y[-1])
plot([xi, xf], [yi, yf], 'ro')
# Vetores velocidade
vi = vector2D(origin=[xi,yi], label=r'$\vec{v}_i$', mpl_options=uvector_style)
vi.polar = (0.5, -dtheta+pi/2)
vi.plot(ax); vi.plot_label(ax, distance=-0.1)
vf = vector2D(origin=[xf,yf], label=r'$\vec{v}_f$', mpl_options=uvector_style)
vf.polar = (0.5, dtheta+pi/2)
vf.plot(ax); vf.plot_label(ax, distance=-0.1)
# Vetores posição
ri = vector2D(dxdy=[xi,yi], label=r'$R$')
ri.plot(ax); ri.plot_label(ax, distance=-0.2)
rf = vector2D(dxdy=[xf,yf])
rf.plot(ax)
rf.plot_angle(ax, length=1.0, distance=-0.45, init_angle=ri.polar[1], label=r'$\theta$')
axis('off')
ax.set_aspect('equal')
- Semelhança de triângulos: $\frac{\Delta r}{r}=\frac{\Delta v}{v}$
- Quando $\Delta t \rightarrow 0$, $L = R\Delta \theta \rightarrow \Delta r$
- $\frac{L}{r}\left(\frac{1}{\Delta t}\right)=\frac{\Delta v}{v}\left(\frac{1}{\Delta t}\right)$, $$ a=\frac{v^2}{r}$$
- Direção de $\Delta \vec{v}$ indica direção de $\vec{a}$. (Por que?)
ax = plt.axes()
# Círculo
theta = linspace(0,2*pi,100)
radius = 1
x = radius*cos(theta) - 1
y = radius*sin(theta)
plot(x,y, 'k:')
# Vetores velocidade
vi = vector2D(origin=[xi,yi], label=r'$\vec{v}_i$', mpl_options=uvector_style)
vi.polar = (0.5, -dtheta+pi/2)
vi.plot(ax); vi.plot_label(ax, distance=-0.1)
vf = vector2D(origin=[xi,yi], label=r'$\vec{v}_f$', mpl_options=uvector_style)
vf.polar = (0.5, dtheta+pi/2)
vf.plot(ax); vf.plot_label(ax, distance=0.2)
vf.plot_angle(ax, length=0.3, distance=-0.1, init_angle=vi.polar[1], label=r'$\theta$')
dv = vector2D(origin=vi.tip, dxdy=vf.dxdy-vi.dxdy, label=r'$\Delta\vec{v}$')
dv.plot(ax); dv.plot_label(ax, distance=-0.1)
# Vetores posição
ri = vector2D(origin=[-1,0], dxdy=[xi,yi], label=r'$\vec{r}_1$')
ri.plot(ax); ri.plot_label(ax, distance=-0.2)
rf = vector2D(origin=[-1,0], dxdy=[xf,yf], label=r'$\vec{r}_2$')
rf.plot(ax); rf.plot_label(ax, distance=0.1)
rf.plot_angle(ax, length=1.0, distance=-0.45, init_angle=ri.polar[1], label=r'$\theta$')
dr = vector2D(origin=ri.tip, dxdy=rf.dxdy-ri.dxdy, label=r'$\Delta\vec{r}$')
dr.plot(ax); dr.plot_label(ax, distance=-0.1)
xlim(-1.1,1.1)
ylim(-1.1,1.1)
axis('off')
ax.set_aspect('equal')
MCU analiticamente¶
- $\vec{r} = x\hat{i} + y \hat{j} = r\cos\theta\hat{i} + r\sin\theta \hat{j}$. $$\vec{r} = r(\cos\theta\hat{i} + \sin\theta \hat{j})\text{, (ou ainda }\vec{r} = r\hat{r})$$
- Num círculo, $r=$cte, enquanto $\theta$ varia entre $[0,2\pi)$.
- No MCU, $\theta(t) = \theta_0 + \omega t$ ($\omega$ = velocidade angular)
- Note que $\frac{d\theta}{dt} = \omega = $ cte
- Então, $$\vec{r} = r[\cos\theta(t)\hat{i} + \sin\theta(t) \hat{j}]$$
ax = plt.axes()
# Círculo
theta = linspace(0,2*pi,100)
radius = 1
theta0 = 0.5
x = radius*cos(theta+theta0)
y = radius*sin(theta+theta0)
plot(x,y, 'k:')
plot([x[0]], [y[0]], 'ro')
# Vetores velocidade
v = vector2D(origin=[x[0],y[0]], label=r'$\vec{v}$', mpl_options=uvector_style)
v.polar = (0.5, theta0+pi/2)
v.plot(ax); v.plot_label(ax, distance=-0.0)
# Vetores posição
r = vector2D(dxdy=[radius,0], mpl_options=line_style)
r.plot(ax)
r = vector2D(dxdy=[x[0],y[0]], label=r'$\vec{r}(t)$')
r.plot(ax); r.plot_label(ax, distance=0.15)
r.plot_angle(ax, length=1.0, distance=-0.45, init_angle=0, label=r'$\theta(t)$')
axis('off')
ax.set_aspect('equal')
$\vec{v}$ no MCU¶
$\vec{a}$ no MCU¶
- Note que $\omega = \frac{v}{r}$, e em termos de $v$,
Representação visual¶
- Abaixo podem ser visualizadas as quantidades vetoriais associadas ao MCU em um ponto típico da trajetória circular
ax = plt.axes()
# Círculo
theta = linspace(0,2*pi,100)
radius = 1
theta0 = 0.5
x = radius*cos(theta+theta0)
y = radius*sin(theta+theta0)
plot(x,y, 'k:')
plot([x[0]], [y[0]], 'ro')
# Vetor posicao
r = vector2D(dxdy=[x[0],y[0]], label=r'$\vec{r}(t)$')
r.plot(ax); r.plot_label(ax, distance=0.15)
# Vetores velocidade
v = vector2D(origin=[x[0],y[0]], label=r'$\vec{v}$', mpl_options=uvector_style)
v.polar = (0.5, theta0+pi/2)
v.plot(ax); v.plot_label(ax, distance=-0.0)
# Vetor aceleração
r = vector2D(origin=[x[0],y[0]], label=r'$\vec{a}(t)$', mpl_options=avector_style)
r.polar= (0.75, theta0+pi)
r.plot(ax); r.plot_label(ax, distance=0.15)
axis('off'); ax.set_aspect('equal')
Movimento relativo (Galileu)¶
- Como dois observadores distintos "percebem" um dado movimento?
- Importante para comparação entre resultados
ax = plt.axes()
coord = array((0.3, 0.2))
ax.add_patch(Rectangle(coord, 0.2, 0.2))
text(0.37, 0.27, r"$o$'")
vo = vector2D(origin=(0.5, 0.3), dxdy=(0.3,0), label=r"$v_{o'o}=80$ km/h")
vo.plot(ax); vo.plot_label(ax, relative_position=0.2,distance=-0.1)
ax.add_patch(Rectangle(coord+array((0.1,0.3)), 0.2, 0.2, fc='r'))
text(0.47, 0.57, r"$P$'")
vo = vector2D(origin=(0.6, 0.6), dxdy=(0.4,0), label=r"$v_{Po}=90$ km/h")
vo.plot(ax); vo.plot_label(ax, relative_position=0.25,distance=-0.1)
xaxis = vector2D(origin=(0.05, 0.05),dxdy=(0.9,0), label=r'$x$')
xaxis.plot(ax); xaxis.plot_label(ax, relative_position=0.9, distance=0.05)
yaxis = vector2D(origin=(0.05, 0.05),dxdy=(0,0.9), label=r'$y$')
yaxis.plot(ax); yaxis.plot_label(ax, relative_position=0.9, distance=-0.05)
text(0.07, 0.07, r'$o$')
axis('off'); ax.set_aspect('equal')
Posição e velocidade relativos (caso geral)¶
- Sejam $\vec{r}_{Po}$ e $\vec{r}_{o'o}$ a posição dos referenciais $P$ e $o'$ em relação à $o$.
- Posição de $P$ relativamente a $o'$: $\vec{r}_{Po'} = \vec{r}_{Po}-\vec{r}_{o'o}$
- Velocidade de $P$ relativamente a $o'$ (derivar eq. acima): $\vec{v}_{Po'} = \vec{v}_{Po}-\vec{v}_{o'o}$, ou $$\vec{v}_{Po} = \vec{v}_{Po'} +\vec{v}_{o'o}.$$
ax = plt.axes()
o = (0.05, 0.05)
opcoord = (0.7, 0.2)
pcoord = (0.5, 0.6)
# Vetores posição
op = vector2D(origin=o, dxdy=opcoord, label=r"$\vec{r}_{o'o}(t)$")
op.plot(ax); op.plot_label(ax, distance=-0.07)
plot(*op.tip, 'ro'); text(*(op.tip+(0.05, 0)), "o'")
p = vector2D(origin=o, dxdy=pcoord, label=r'$\vec{r}_{Po}(t)$')
p.plot(ax); p.plot_label(ax, distance=0.15)
plot(*p.tip, 'ro'); text(*(p.tip+(0.05, 0)), 'P')
pop = vector2D(origin=op.tip, dxdy=p.dxdy-op.dxdy, label=r"$\vec{r}_{Po'}(t)=\vec{r}_{Po}(t)-\vec{r}_{o'o}(t)$")
pop.plot(ax); pop.plot_label(ax, distance=-0.1)
xaxis = vector2D(origin=o,dxdy=(0.9,0), label=r'$x$')
xaxis.plot(ax); xaxis.plot_label(ax, relative_position=0.9, distance=0.05)
yaxis = vector2D(origin=o,dxdy=(0,0.9), label=r'$y$')
yaxis.plot(ax); yaxis.plot_label(ax, relative_position=0.9, distance=-0.05)
xlim(0,1); ylim(0,1)
axis('off'); ax.set_aspect('equal')
Aceleração relativa¶
- Aceleração $P$ relativamente a $o'$: $\vec{a}_{Po'} = \vec{a}_{Po}-\vec{a}_{o'o}$, ou $$\vec{a}_{Po} = \vec{a}_{Po'} +\vec{a}_{o'o}.$$
R.: Se a velocidade relativa $\vec{v}_{Po'}=$cte, então $\vec{a}_{Po'}=0$ e $\vec{a}_{Po} = \vec{a}_{o'o}.$ As leis de Newton só são válidas em referenciais inerciais (não acelerados).


